【導讀】高斯濾波器是一種線性濾波器,能夠有效的抑制噪聲,平滑圖像。其作用原理和均值濾波器類似,都是取濾波器窗口內的像素的均值作為輸出。本文主要介紹了高斯濾波器的原理及其實現過程。
其窗口模板的系數和均值濾波器不同,均值濾波器的模板系數都是相同的為1;而高斯濾波器的模板系數,則隨著距離模板中心的增大而系數減小。所以,高斯濾波器相比于均值濾波器對圖像個模糊程度較小。
什么是高斯濾波器
既然名稱為高斯濾波器,那么其和高斯分布(正態分布)是有一定的關系的。一個二維的高斯函數如下:
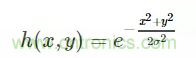
其中(x,y)(x,y)為點坐標,在圖像處理中可認為是整數;σσ是標準差。要想得到一個高斯濾波器的模板,可以對高斯函數進行離散化,得到的高斯函數值作為模板的系數。例如:要產生一個3×33×3的高斯濾波器模板,以模板的中心位置為坐標原點進行取樣。模板在各個位置的坐標,如下所示(x軸水平向右,y軸豎直向下)
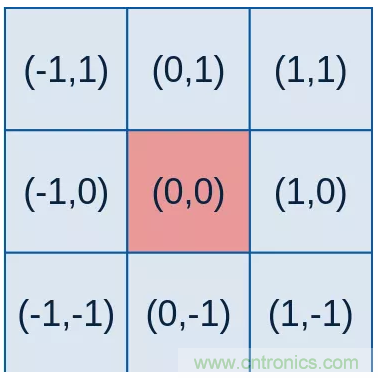
這樣,將各個位置的坐標帶入到高斯函數中,得到的值就是模板的系數。
對于窗口模板的大小為(2k+1)×(2k+1),模板中各個元素值的計算公式如下:
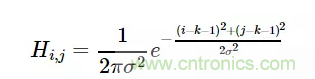
這樣計算出來的模板有兩種形式:小數和整數。
小數形式的模板,就是直接計算得到的值,沒有經過任何的處理;
整數形式的,則需要進行歸一化處理,將模板左上角的值歸一化為1,下面會具體介紹。使用整數的模板時,需要在模板的前面加一個系數,系數為
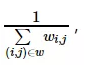
也就是模板系數和的倒數。
高斯模板的生成
知道模板生成的原理,實現起來也就不困難了
void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
static const double pi = 3.1415926;
int center = ksize / 2; // 模板的中心位置,也就是坐標的原點
double x2, y2;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - center, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - center, 2);
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
g /= 2 * pi * sigma;
window[i][j] = g;
}
}
double k = 1 / window[0][0]; // 將左上角的系數歸一化為1
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
window[i][j] *= k;
}
}
}
需要一個二維數組,存放生成的系數(這里假設模板的最大尺寸不會超過11);第二個參數是模板的大小(不要超過11);第三個參數就比較重要了,是高斯分布的標準差。
生成的過程,首先根據模板的大小,找到模板的中心位置ksize/2。然后就是遍歷,根據高斯分布的函數,計算模板中每個系數的值。
需要注意的是,最后歸一化的過程,使用模板左上角的系數的倒數作為歸一化的系數(左上角的系數值被歸一化為1),模板中的每個系數都乘以該值(左上角系數的倒數),然后將得到的值取整,就得到了整數型的高斯濾波器模板。
下面截圖生成的是,大小為3×3,σ=0.83×3,σ=0.8的模板
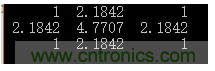
對上述解結果取整后得到如下模板:
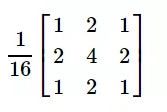
這個模板就比較熟悉了,其就是根據σ=0.8的高斯函數生成的模板。
至于小數形式的生成也比較簡單,去掉歸一化的過程,并且在求解過程后,模板的每個系數要除以所有系數的和。具體代碼如下:
void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
static const double pi = 3.1415926;
int center = ksize / 2; // 模板的中心位置,也就是坐標的原點
double x2, y2;
double sum = 0;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - center, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - center, 2);
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
g /= 2 * pi * sigma;
sum += g;
window[i][j] = g;
}
}
//double k = 1 / window[0][0]; // 將左上角的系數歸一化為1
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
window[i][j] /= sum;
}
}
}
3×3,σ=0.8的小數型模板。
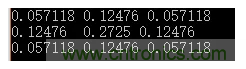
σσ值的意義及選取
通過上述的實現過程,不難發現,高斯濾波器模板的生成最重要的參數就是高斯分布的標準差σσ。標準差代表著數據的離散程度,如果σσ較小,那么生成的模板的中心系數較大,而周圍的系數較小,這樣對圖像的平滑效果就不是很明顯;反之,σσ較大,則生成的模板的各個系數相差就不是很大,比較類似均值模板,對圖像的平滑效果比較明顯。
來看下一維高斯分布的概率分布密度圖:
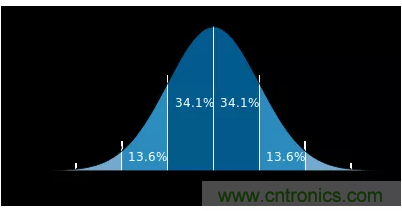
橫軸表示可能得取值x,豎軸表示概率分布密度F(x),那么不難理解這樣一個曲線與x軸圍成的圖形面積為1。σσ(標準差)決定了這個圖形的寬度,可以得出這樣的結論:σσ越大,則圖形越寬,尖峰越小,圖形較為平緩;σσ越小,則圖形越窄,越集中,中間部分也就越尖,圖形變化比較劇烈。這其實很好理解,如果sigma也就是標準差越大,則表示該密度分布一定比較分散,由于面積為1,于是尖峰部分減小,寬度越寬(分布越分散);同理,當σσ越小時,說明密度分布較為集中,于是尖峰越尖,寬度越窄!
于是可以得到如下結論:
σσ越大,分布越分散,各部分比重差別不大,于是生成的模板各元素值差別不大,類似于平均模板;
σσ越小,分布越集中,中間部分所占比重遠遠高于其他部分,反映到高斯模板上就是中心元素值遠遠大于其他元素值,于是自然而然就相當于中間值得點運算。
基于OpenCV的實現
在生成高斯模板好,其簡單的實現和其他的空間濾波器沒有區別,具體代碼如下:
void GaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
CV_Assert(src.channels() || src.channels() == 3); // 只處理單通道或者三通道圖像
const static double pi = 3.1415926;
// 根據窗口大小和sigma生成高斯濾波器模板
// 申請一個二維數組,存放生成的高斯模板矩陣
double **templateMatrix = new double*[ksize];
for (int i = 0; i < ksize; i++)
templateMatrix[i] = new double[ksize];
int origin = ksize / 2; // 以模板的中心為原點
double x2, y2;
double sum = 0;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - origin, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - origin, 2);
// 高斯函數前的常數可以不用計算,會在歸一化的過程中給消去
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
sum += g;
templateMatrix[i][j] = g;
}
}
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
templateMatrix[i][j] /= sum;
cout << templateMatrix[i][j] << " ";
}
cout << endl;
}
// 將模板應用到圖像中
int border = ksize / 2;
copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
int channels = dst.channels();
int rows = dst.rows - border;
int cols = dst.cols - border;
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int a = -border; a <= border; a++)
{
for (int b = -border; b <= border; b++)
{
if (channels == 1)
{
sum[0] += templateMatrix[border + a][border + b] * dst.at<uchar>(i + a, j + b);
}
else if (channels == 3)
{
Vec3b rgb = dst.at<Vec3b>(i + a, j + b);
auto k = templateMatrix[border + a][border + b];
sum[0] += k * rgb[0];
sum[1] += k * rgb[1];
sum[2] += k * rgb[2];
}
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i, j) = rgb;
}
}
}
// 釋放模板數組
for (int i = 0; i < ksize; i++)
delete[] templateMatrix[i];
delete[] templateMatrix;
}
只處理單通道或者三通道圖像,模板生成后,其濾波(卷積過程)就比較簡單了。不過,這樣的高斯濾波過程,其循環運算次數為m×n×ksize2,其中m,n為圖像的尺寸;ksize為高斯濾波器的尺寸。這樣其時間復雜度為O(ksize2),隨濾波器的模板的尺寸呈平方增長,當高斯濾波器的尺寸較大時,其運算效率是極低的。為了,提高濾波的運算速度,可以將二維的高斯濾波過程分解開來。
分離實現高斯濾波
由于高斯函數的可分離性,尺寸較大的高斯濾波器可以分成兩步進行:首先將圖像在水平(豎直)方向與一維高斯函數進行卷積;然后將卷積后的結果在豎直(水平)方向使用相同的一維高斯函數得到的模板進行卷積運算。具體實現代碼如下:
// 分離的計算
void separateGaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
CV_Assert(src.channels()==1 || src.channels() == 3); // 只處理單通道或者三通道圖像
// 生成一維的高斯濾波模板
double *matrix = new double[ksize];
double sum = 0;
int origin = ksize / 2;
for (int i = 0; i < ksize; i++)
{
// 高斯函數前的常數可以不用計算,會在歸一化的過程中給消去
double g = exp(-(i - origin) * (i - origin) / (2 * sigma * sigma));
sum += g;
matrix[i] = g;
}
// 歸一化
for (int i = 0; i < ksize; i++)
matrix[i] /= sum;
// 將模板應用到圖像中
int border = ksize / 2;
copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
int channels = dst.channels();
int rows = dst.rows - border;
int cols = dst.cols - border;
// 水平方向
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int k = -border; k <= border; k++)
{
if (channels == 1)
{
sum[0] += matrix[border + k] * dst.at<uchar>(i, j + k); // 行不變,列變化;先做水平方向的卷積
}
else if (channels == 3)
{
Vec3b rgb = dst.at<Vec3b>(i, j + k);
sum[0] += matrix[border + k] * rgb[0];
sum[1] += matrix[border + k] * rgb[1];
sum[2] += matrix[border + k] * rgb[2];
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i, j) = rgb;
}
}
}
// 豎直方向
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int k = -border; k <= border; k++)
{
if (channels == 1)
{
sum[0] += matrix[border + k] * dst.at<uchar>(i + k, j); // 列不變,行變化;豎直方向的卷積
}
else if (channels == 3)
{
Vec3b rgb = dst.at<Vec3b>(i + k, j);
sum[0] += matrix[border + k] * rgb[0];
sum[1] += matrix[border + k] * rgb[1];
sum[2] += matrix[border + k] * rgb[2];
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i, j) = rgb;
}
}
}
delete[] matrix;
}
代碼沒有重構較長,不過其實現原理是比較簡單的。首先得到一維高斯函數的模板,在卷積(濾波)的過程中,保持行不變,列變化,在水平方向上做卷積運算;接著在上述得到的結果上,保持列不邊,行變化,在豎直方向上做卷積運算。這樣分解開來,算法的時間復雜度為O(ksize)O(ksize),運算量和濾波器的模板尺寸呈線性增長。
在OpenCV也有對高斯濾波器的封裝GaussianBlur,其聲明如下:
CV_EXPORTS_W void GaussianBlur( InputArray src, OutputArray dst, Size ksize,
double sigmaX, double sigmaY = 0,
int borderType = BORDER_DEFAULT );
二維高斯函數的標準差在x和y方向上應該分別有一個標準差,在上面的代碼中一直設其在x和y方向的標準是相等的,在OpenCV中的高斯濾波器中,可以在x和y方向上設置不同的標準差。
下圖是自己實現的高斯濾波器和OpenCV中的GaussianBlur的結果對比
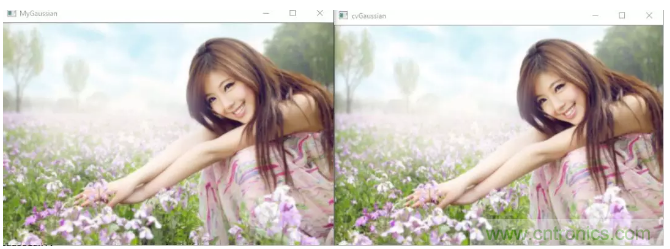
上圖是5×5,σ=0.8的高斯濾波器,可以看出兩個實現得到的結果沒有很大的區別。
總結
高斯濾波器是一種線性平滑濾波器,其濾波器的模板是對二維高斯函數離散得到。由于高斯模板的中心值最大,四周逐漸減小,其濾波后的結果相對于均值濾波器來說更好。
高斯濾波器最重要的參數就是高斯分布的標準差σσ,標準差和高斯濾波器的平滑能力有很大的能力,σσ越大,高斯濾波器的頻帶就較寬,對圖像的平滑程度就越好。通過調節σσ參數,可以平衡對圖像的噪聲的抑制和對圖像的模糊。







